Как рассчитать крутящий момент на колесе, Мощность момент — Энциклопедия журнала "За рулем"

Что касается крутящего момента, определяемого на выходе редуктора M2 , то этот показатель можно получить, умножив номинальный параметр Mn2 на передаточное число устройства. Крутящий момент мотор-колеса электрического велосипеда отвечает за способность ускорятся и преодолевать препятствия. Нарушение авторских прав будет рассматриваться согласно статьи 52 Закона Украины «О авторском праве и смежных правах», статьи Криминального Кодекса Украины, статьи Гражданского кодекса Украины, статьи Кодекса Украины об административных правонарушениях.
Исходя из того что момент на последнем валу нам известен момент на выходном валу —можно по формуле 9 рассчитать моменты на стальных валах. Нсм Нсм Нсм Нсм Нсм 0. Примем следующие коэффициенты , ,. Вычислим значение модуля при расчете на контактное напряжение по формуле 1 0 :. Эквивалентное число зубьев шестерни и колеса для прямозубой цилиндрической передачи: Z ЭКВ.
Определим слабое звено. Слабым звеном является колесо, поэтому в формулу 11 подставляем его параметры. Ширина b для всех колес одинакова и равна:. Диаметры делительной окружности, окружности выступов и окружности впадин вычисляются по следующим формулам:. Рассчитаем диаметр делительной окружности, окружности выступов и окружности впадин для колеса на выходном валу.
Колесо Число зубьев Размеры в мм D d a D f b Z 1 20 12 13,2 10,5 5,8 Z 2 43 25,8 27 24,3 4,8 Z 3 18 10,8 12 9,3 5,8 Z 4 72 43,2 43,4 41,7 4,8 Z 5 18 10,8 12 9,3 5,8 Z 6 90 54 55,2 52,5 4,8 Z 7 18 10,8 12 9,3 5,8 Z 8 90 54 55,2 52,5 4,8. Рассмотрим плоскость XOZ Рис. Кроме распорных и окружных сил в зацеплениях на выходной вал действуют радиальная Pko ,Н и окружная Pkr ,Н силы со стороны кулачка.
Профиль кулачка представлен на рисунке 5. Силы определяются по формулам 18 , 20 при их определении учитывается то , что плоскости зацеплений на валу и плоскость контакта кулачка с толкателем находятся по углом 45 градусов.
C илы Px и Pkx рассчитываются по формулам.
Вычислим силы Px и Pkx. Из основных уравнений механики следует ,что :. Py равно распорной силе, следовательно. Для наглядности расчетов на рисунке 8 показано взаимное расположение зацеплений на предвыходном валу.
Получим выражения для Px и Prx пользуясь формулой Вычислим значения этих величин. Решая данную систему уравнений найдем реакции в опорах:. Получим выражения для Py и Pry пользуясь формулой Изгибающие моменты на входном валу XOZ.
Опасным сечением по полученным эпюрам является сечение для выходного и предвыходного вала. Определим суммарный изгибающий момент в этих сечениях.
Принимаем: мм, мм. Исходя из рассчитанных диаметров валов и справочных данных выберем подшипники для выходного и предвыходного валов. Радиальную силу действующую на подшипник определим как максимальную реакцию опоры:.
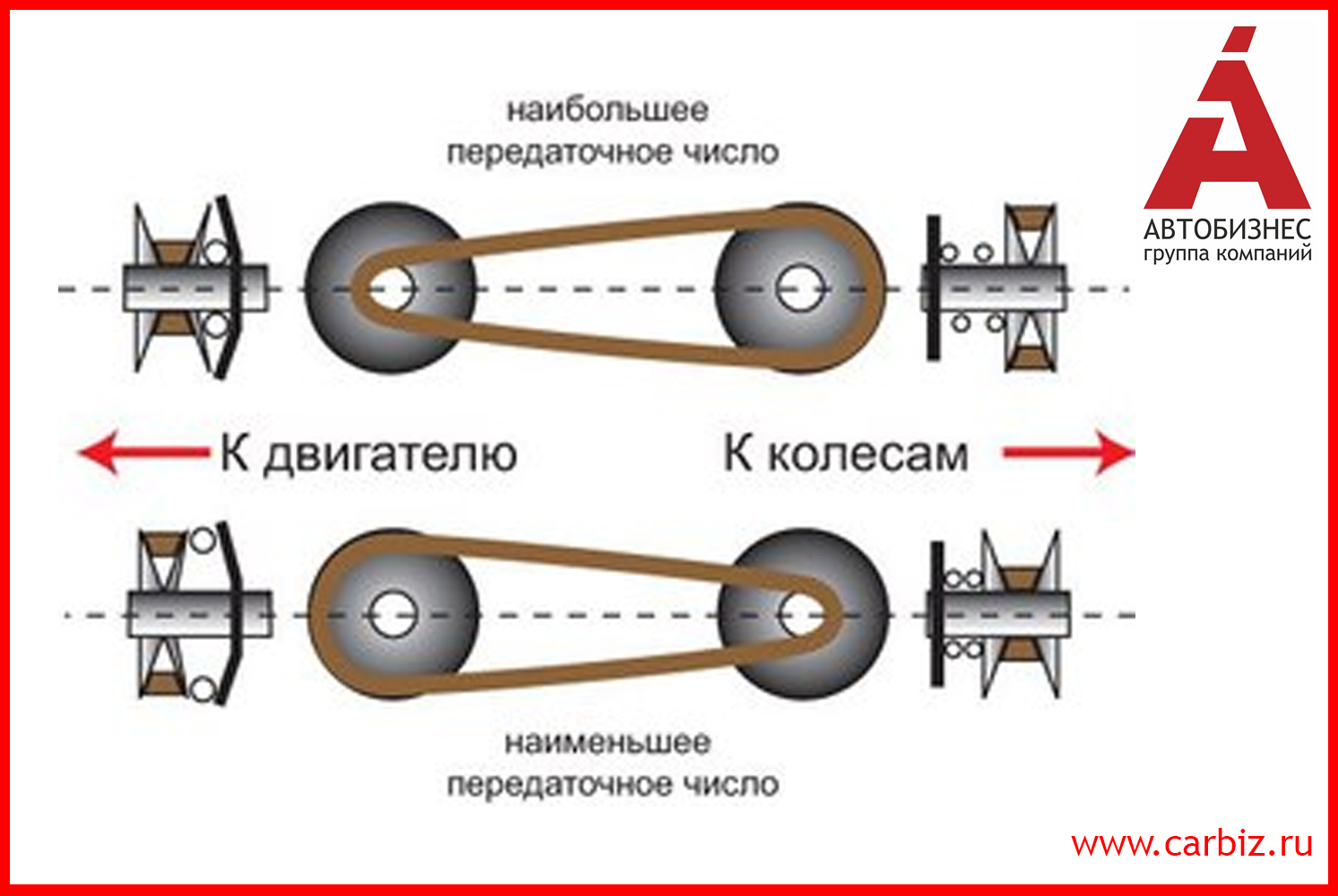
Максимальные скорости на третьей и пятой передачах V 3 и V 5 существенно ниже. Но на спуске или с ветром вдогон выгодней может стать пятая передача, а на подъеме или с ветром в лоб — третья. Другие враги скорости — подъем дороги и встречный ветер. Но еще коварней ветер. Его скорость сложится со скоростью машины относительно дороги, — и уже эту сумму в расчете затрат мощности надо возвести в куб! Но придуманный нами автомобиль так ехать не может… Маловато мощи!
М5 или тяговая сила F тяг 1 …F тяг 5 на ведущей оси от включенной передачи. На рис. Величины сил — на вертикальной оси справа. Но тут важно учесть следующее.
Разгоняет машину не вся тяговая сила, а лишь избыточная — то есть разница между полной тяговой силой колес и сопротивлением воздуха. Отношение этой силы к весу машины академик Чудаков назвал динамическим фактором D. На первой передаче сопротивление воздуха мало, его можно не учитывать — считать, что машину разгоняет полная сила F тяг.
Но отталкиваться от дороги сильней, чем позволяет сцепление шин, невозможно! Это неплохо согласуется с такой официальной характеристикой любого автомобиля как предельно возможный угол подъема. С «моноприводом» трудно получить больше. Правда, у машины с задним приводом на подъемах ведущие колеса несколько догружаются весом машины, а вот передний тут невыгоден. Лучшая схема, но сложная и дорогая, — полный привод конечно, не с такой скромной мощностью, как у «Нивы» или УАЗа! Если избыточная сила на первой передаче, например слишком велика, машина «шлифует» дорогу.
Дело нелепое, нужно перейти на следующую передачу. А вот при разработке нового авто конструктор учитывает высокую мощность двигателя и ее следствие — тяговые силы в передаточных числах трансмиссии. Передачи проектируются как достаточно «длинные», расширяющие диапазон скоростей при достаточных ускорениях. А это значит, что и при более высоких скоростях действуют нужные тяговые силы или моменты на колесах.
Иначе говоря, реализуется весь арсенал мощности! Значит, она все же важнее. Споры на тему влияния мощности-момента ведутся давно, и конца им не видно. Вроде бы сто раз уже объясняли самыми разными способами, что тут к чему, а воз и ныне там. Вызывает неподдельный интерес, откуда все же берется заблуждение и почему оно такое устойчивое?
Причин видится две. Одна из них в том, что мощность есть функция от момента. Зависимость мощности от момента стоит барьером, который преодолеть оказывается непросто. Что странно. Поскольку очевидность того, что мощность есть функция не только от момента, но и от оборотов, не оспаривается, и тот факт, что у разных двигателей бывает весьма большой разброс по соотношению мощности к моменту, также не подвергается сомнению.
То есть существует молчаливое согласие с тем, что мощность есть функция от двух аргументов - оборотов и момента, но при этом зависимость от оборотов как бы игнорируется. А в этом и есть вторая, главная причина заблуждения. И ключевая фраза здесь: "Человек совершенно может не иметь понятие про мощность. А вот разницу в ускорении на 3 и 4 передаче он вполне способен почувствовать. На графике 1 видны кривые мощности двигателя, смещенные в зависимости от разных передаточных чисел и кривая сопротивлений.
Видно, что с ростом передаточного числа динамика резко возрастает. Это очевидно и вопросов не вызывает. Странно, что не менее очевидный факт, что бОльшая часть времени при разгоне приходится вовсе не на 1 и 2 передачи, а на , при этом упускается из виду.
При разгоне здравомыслящий водитель пользуется всеми четырьмя передачами и весьма широким диапазоном частот вращения двигателя. При этом редко задумывается о том, что динамика разгона на высокой скорости мала и плохо ощущается, но именно на нее и приходится львиная доля времени разгона по той простой причине, повторю, что на высших передачах динамика хуже и потому занимает больше времени.
Хорошо ощущается динамика разгона на низших передачах, в диапазоне низких и средних оборотов дальше водитель двигатель раскручивает редко. И что выходит?
А выходит, что "низовой", моментный двигатель дает ощущение уверенного и бодрого разгона по той простой причине, что легко и весело страгивает и начинает разгонять автомобиль.
А по достижении скорости ощущения становятся слабыми, и оценить разницу в разгоне и сильного моторов на передачах, способен не каждый. Потому и кажется, что момент определяет динамику. По ощущениям. А ощущениям человек склонен верить очень сильно, даже вопреки логике и здравому смыслу. Проповедующие формулировку "скорость определяется мощностью, а динамика разгона - моментом двигателя" могут убедиться в своем заблуждении, решив простую задачу. Вводные 1. Поднимаем равномерно груз весом 75 кг на высоту 1 м за 1 с.
Какая мощность должна быть в моторе, спрятанном внутри черного ящика? Какой момент должен быть в моторе, спрятанном внутри черного ящика?
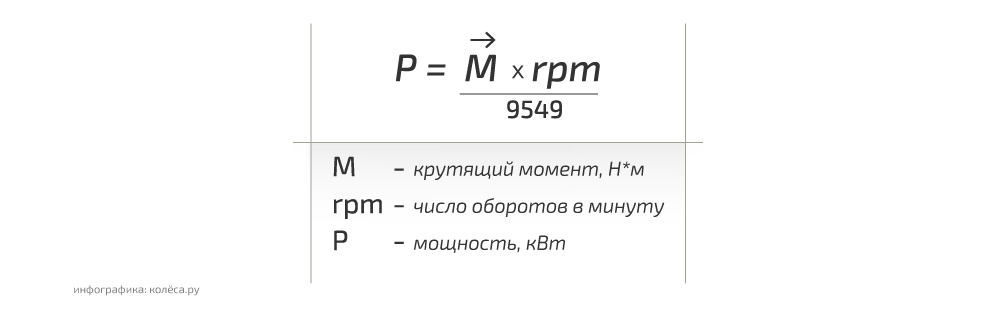
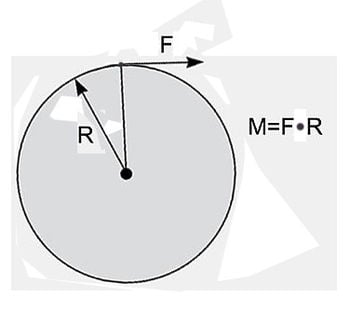
В этом случае, радиус колеса является расстоянием силы от центра вращения. В примере с рукой робота, удерживающей объект, мы можем рассчитать крутящий момент, требуемый для поднятия объекта.
Если объект обладает массой, равной 1 ньютону, а рука имеет длину 0,25 метра объект располагается на расстоянии 0,25 метра от центра вращения , тогда. Это означает, что для удержания объекта в неподвижном положении, необходимо применить крутящий момент, равный 0,25 ньютон-метров. Чтобы переместить объект вверх, роботу необходимо приложить к нему крутящий момент, значение которого будет превышать 0,25 ньютон-метров, так как необходимо преодолеть силу гравитации.
Чем больше крутящий момент робота, тем больше силы он прикладывает к объекту, тем больше ускорение объекта, и тем быстрее рука поднимет объект.
Для данного примера, длина рука равна половине длины руки из Примера 1, поэтому значение требуемого крутящего момента также в два раза меньше. Значение длины руки пропорционально значению требуемого крутящего момента.
При равных исходных характеристиках объекта, чем короче рука, тем меньший крутящий момент необходим для подъема. Для данного примера, длина рука равна удвоенной длине руки из Примера 1, поэтому значение требуемого крутящего момента также в два раза больше. Еще одна точка зрения относительно ограниченного крутящего момента в соединении руки робота заключается в следующем: более короткая рука сможет поднять объект большей массы, чем более длинная рука; однако, для первой доступная высота подъема объекта будет меньше, чем для второй.
Эти примеры иллюстрируют руку робота, поднимающую объекты разной массы. Какова взаимосвязь с требуемым количеством крутящего момента?
Эти примеры иллюстрируют уменьшение значения требуемого крутящего момента по мере снижения массы объекта. Масса пропорциональна крутящему моменту, необходимому для ее подъема. Чем тяжелее объект, тем больше крутящий момент, требуемый для его подъема. Проектировщики роботов должны обратить внимание на ключевые взаимосвязи между значениями крутящего момента, длины руки и массы объекта.
Например, для удерживания объекта необходимо 10 фунтов силы. Далее, чтобы поднять этот объект на высоту 10 дюймов, требуется определенное количество работы. Количество работы, требуемое для подъема объекта на высоту 20 дюймов, удваивается.